Teorema de Miquel

En geometría plana, los teoremas de Miquel son una serie de proposiciones relacionadas con circunferencias concurrentes. Deben su nombre al matemático francés Auguste Miquel (1816-1851).

Enunciados

NOTA: en el presente artículo se utiliza en ocasiones la palabra círculo con el sentido de circunferencia, debido a que en la fuente original francesa no se hace distinción entre ambos términos (aunque en sentido estricto, en español debería usarse el término circunferencia, porque es este el concepto que se está manejando).

Teorema de los tres círculos

Considérense tres circunferencias (C1), (C2) y (C3), que se encuentran en un punto M; y se denominan D, E y F a los demás puntos de intersección de las circunferencias (C2) y (C3), (C3) y (C1 ), (C1) y (C2) respectivamente. Sea A un punto de (C1) tal que la recta (FA) interseca a (C2) en B y tal que la recta (EA) interseca a (C3) en C. Entonces, los puntos B, D y C están alineados.

Recíproco: si ABC es un triángulo, y si D, E y F son tres puntos situados respectivamente en (BC), (CA) y (AB), entonces las circunferencias circunscritas de los triángulos AEF, BDF y CDE se cruzan en un punto M.[1][2][3][4]

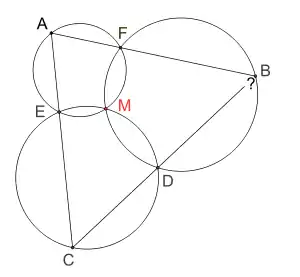
Teorema del cuadrilátero completo

Si ABCDEF es un cuadrilátero completo, entonces las circunferencias circunscritas de los triángulos EAD, EBC, FAB y FDC convergen en un punto M llamado punto de Miquel.

Demostrado en 1838 por A. Miquel, este resultado fue denominado teorema del pivote por Forder.[5]

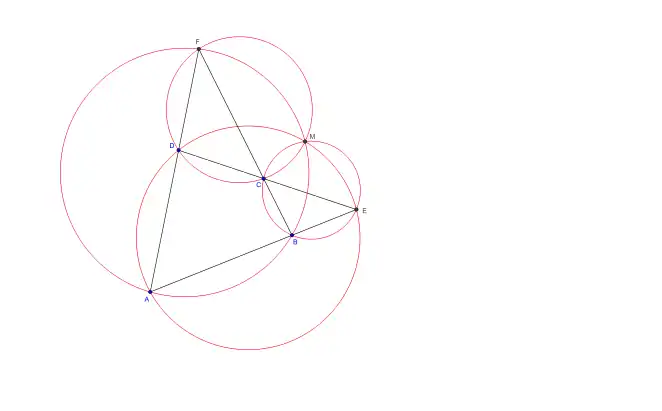
Círculo de Miquel

Los centros O1, O2, O3 y O4 de las cuatro circunferencias y el punto de Miquel M son cocíclicos.

La circunferencia que contiene estos cinco puntos se conoce como círculo de Miquel.

Teorema de los cuatro círculos

Sean (C1), (C2), (C3) y (C4) cuatro circunferencias. Se denomina respectivamente A1 y B1 a las intersecciones de (C1) y (C2); A2 y B2 a los puntos de intersección de (C2) y (C3); A3 y B3 a las intersecciones de (C3) y (C4); y A4 y B4 a las intersecciones de (C1) y (C4). Los puntos A1, A2, A3 y A4 están alineados o son cocíclicos si y solo si ocurre lo mismo con los puntos B1, B2, B3 y B4.

Teorema del pentágono

Sea ABCDE un pentágono cualquiera. Si F, G, H, I, J son los puntos de intersección de los lados (EA) y (BC), (AB) y (CD), (BC) y (DE), (CD) y (EA), (DE) y (AB) respectivemente, entonces los puntos de intersección de las cinco circunferencias circunscritas ABF, BCG, CDH, DEI y EAJ están situados sobre una sexta circunferencia.

Teorema de los cinco círculos (o de los seis círculos)

Si (C1), (C2), (C3), (C4) y (C5) son cinco circunferencias cuyos centros se hallan sobre una circunferencia (C) y que se cruzan entre vecinos en (C). Entonces, las cinco rectas que unen los puntos de intersección no ubicados en (C) de cada circunferencia con sus circunferencias vecinas, se encuentran en las circunferencias.

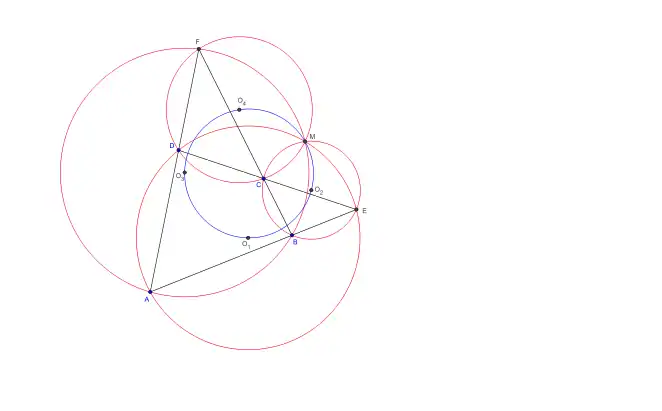
Comentarios históricos
  • Auguste Miquel publicó parte de estos teoremas en los cuadernos de Liouville (Journal of Pure and Applied Mathematics) en 1838.
  • El primer teorema de Miquel es un resultado clásico conocido mucho antes que él usando ángulo inscrito.
  • El teorema de los cinco círculos (o de los seis círculos) es un caso especial de un teorema general enunciado y demostrado por el matemático William Kingdon Clifford. Este problema volvió a estar de moda tras un desafío lanzado en 2002 por el presidente chino Jiang Zemin durante un congreso de matemáticos en Pekín en 2002. Fue retomado por Alain Connes durante un seminario en de octubre de 2002.

Referencias
  1. Mohammed AASSILA (2018). «32». En Ellipses, ed. 1000 challenges mathématiques, géométrie.
  2. David Acheson (2021). «272». En Flamarion, ed. Géométrix, d'Euclide à Einstein, la magie d'une science surprenante.
  3. David Wells (1995). «135». En Eyrolles, ed. Le dictionnaire Penguin des curiosités géométriques.
  4. Yvonne et René Sortais (1987). «58-65». En Hermann, ed. La géométrie du triangle.
  5. Jean Louis Ayme, Auguste Miquel, p.6

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.