Mapa regular (teoría de grafos)

En matemáticas, un mapa regular es un teselado simétrico de una superficie cerrada. Más precisamente, es una descomposición de una variedad bidimensional (como una esfera, un toro o un plano proyectivo) en discos topológicos de tal manera que cada bandera (una triple incidencia de vértice-arista-cara) se puede transformar en cualquier otra bandera mediante una simetría de la descomposición. Los mapas regulares son, en cierto sentido, generalizaciones topológicas de los sólidos platónicos. La teoría de mapas y su clasificación está relacionada con la teoría de las superficies de Riemann, la geometría hiperbólica y la teoría de Galois. Los mapas regulares se clasifican según: el genus y la orientabilidad de la superficie de apoyo, el grafo subyacente o el grupo de automorfismos.

El hosoedro hexagonal, un mapa regular sobre la esfera con dos vértices, seis aristas, seis caras y 24 banderas

El mapa regular {6,3}_4,0 sobre un toro, con 16 caras, 32 vértices y 48 aristas

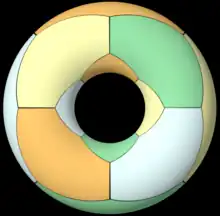
Resumen

Los mapas regulares generalmente se definen y estudian de tres maneras: topológicamente, en teoría de grupos y en teoría de grafos.

Enfoque topológico

Topológicamente, un mapa es una descomposición 2-celdas de una 2-variedad compacta y cerrada.

El genus g de un mapa M viene dado por la relación de Euler $\chi (M)=|V|-|E|+|F|$ que es igual a $2-2g$ si el mapa es orientable, y $2-g$ si el mapa no es orientable. Es un hecho crucial que hay un número finito (distinto de cero) de mapas regulares para cada género orientable, excepto el toro.

Enfoque en teoría de grupos

En teoría de grupos, la representación de permutación de un mapa regular M es un grupo de permutación C transitivo, sobre un conjunto $\Omega$ de banderas, generado por tres involuciones libres de puntos fijos r₀, r₁ y r₂, que satisface (r₀r₂)²= I. En esta definición, las caras son las órbitas de F = <r₀, r ₁>, las aristas son las órbitas de E = <r₀, r₂>, y los vértices son las órbitas de V = <r₁, r₂>.

De manera más abstracta, el grupo de automorfismos de cualquier mapa regular es la imagen homomórfica no degenerada de un <2,m,n>-grupo triangular.

Enfoque en teoría de grafos

Teóricamente, un mapa es un grafo cúbico $\Gamma$ con aristas de color azul, amarillo o rojo, tal que: $\Gamma$ es conexo, cada vértice incide en una arista de cada color, y los ciclos de aristas que no son de color amarillo tienen una longitud de 4. Téngase en cuenta que $\Gamma$ es el grafo de banderas o mapa de grafo codificado (GEM) del mapa, definido en el conjunto de vértices de banderas $\Omega$ y no es el esqueleto G= (V,E) del mapa. En general,| $\Omega$ |= 4|E|.

Un mapa M es regular si Aut(M) actúa regularmente en las banderas. Aut(M) de un mapa regular es transitivo en los vértices, aristas y caras de M. Se dice que una función M es reflexiva si Aut(M) es regular y contiene un automorfismo $\phi$ que fija tanto un vértice v como una cara f, pero invierte el orden de las aristas. Un mapa que es regular pero no reflexivo se dice que es quiral.

Ejemplos

El hemicubo, un mapa regular

El gran dodecaedro es un mapa regular con caras pentagonales en una superficie orientable de género 4.
El hemicubo es un mapa regular de tipo {4,3} en el plano proyectivo.
El hemidodecaedro es un mapa regular producido por la incrustación pentagonal del grafo de Petersen en el plano proyectivo.
El p-hosoedro es un mapa regular de tipo {2,p}.
El grafo de Dyck es un mapa regular de 12 octágonos en una superficie de género 3. Su grafo subyacente, el grafo de Dyck, también puede formar un mapa regular de 16 hexágonos en un toro.

La siguiente es una lista completa de mapas regulares en superficies de característica de Euler, χ positiva: la esfera y el plano proyectivo.[1]

χ	g	Schläfli	Vértices	Aristas	Caras	Grupo	Orden	Grafo	Notas
2	0	{p,2}	p	p	2	C₂ × Diedral_p	4p	C_p	Diedro
2	0	{2,p}	2	p	p	C₂ × Dih_p	4p	p-fold K₂	Hosoedro
2	0	{3,3}	4	6	4	S₄	24	K₄	Tetraedro
2	0	{4,3}	8	12	6	C₂ × S₄	48	K₄ × K₂	Cubo
2	0	{3,4}	6	12	8	C₂ × S₄	48	K_2,2,2	Octaedro
2	0	{5,3}	20	30	12	C₂ × A₅	120		Dodecaedro
2	0	{3,5}	12	30	20	C₂ × A₅	120	K₆ × K₂	Icosaedro
1	n1	{2p,2}/2	p	p	1	Dih_2p	4p	C_p	Hemi-dihedron[2]
1	n1	{2,2p}/2	2	p	p	Dih_2p	4p	p-fold K₂	Hemi-hosohedron[2]
1	n1	{4,3}/2	4	6	3	S₄	24	K₄	Hemicubo
1	n1	{3,4}/2	3	6	4	S₄	24	2-fold K₃	Hemioctaedro
1	n1	{5,3}/2	10	15	6	A₅	60	Grafo de Petersen	Hemidodecaedro
1	n1	{3,5}/2	6	15	10	A₅	60	K₆	Hemiicosaedro

Las imágenes a continuación muestran tres de los 20 mapas regulares en el toro triple, etiquetados con sus símbolos de Schläfli.

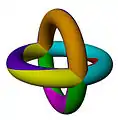{6,4}
{4,8}
{8,4}

Poliedros toroidales

Ejemplos visualizados como redes
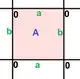{4,4}_{1,0 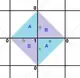(v:1, e:2, f:1)}	{4,4}_1,1 (v:2, e:4, f:2)	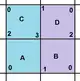{4,4}_2,0 (v:4, e:8, f:4)	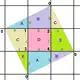{4,4}_2,1 (v:5, e:10, f:5)	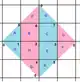{4,4}_{2,2 (v:8, e:16, f:8)}
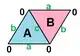{3,6}_1,0 (v:1, e:3, f:2)	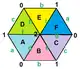{3,6}_1,1 (v:3, e:9, f:6)	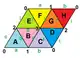{3,6}_2,0 (v:4, e:12, f:8)	{3,6}_{2,1 (v:7, e:21, f:14)}	{3,6}_2,2 (v:12, e:36, f:24)
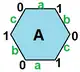{6,3}_1,0 (v:2, e:3, f:1)	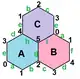{6,3}_1,1 (v:6, e:9, f:3)	{6,3}_{2,0 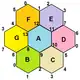(v:8, e:12, f:4)}	{6,3}_2,1 (v:14, e:21, f:7)	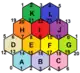{6,3}_2,2 (v:24, e:36, f:12)

Los mapas regulares existen como poliedros toroédricos como porciones finitas de mosaicos euclídeos, envueltos en la superficie de un duocilindro como un toro. Están etiquetados como {4,4}_b,c para aquellas formas relacionadas con el teselado cuadrado, {4,4}.[3] las del tipo {3,6}_b,c están relacionadas con el teselado triangular, y las del tipo {3,6} y {6,3}_b,c están relacionadas con el teselado hexagonal, {6,3}. Los valores b y c son números naturales.[4] Hay 2 casos especiales (b,0) y (b,b) con simetría reflexiva, mientras que los casos generales existen en pares quirales (b, c) y (c,b).

Los mapas regulares de la forma {4,4}_m,0 se pueden representar como el poliedro oblicuo regular finito {4,4|m}, visto como las caras cuadradas de un m×m duoprisma en 4 dimensiones.

Aquí hay un ejemplo {4,4}_8,0 generado a partir de un plano configurado como un tablero de ajedrez, transformado primero en cilindro y después en un toro. La proyección de un cilindro a un toro distorsiona la geometría en 3 dimensiones, pero se puede realizar sin distorsión en 4 dimensiones.

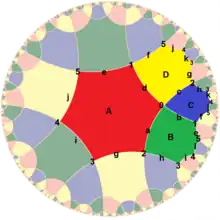Por ejemplo, el mapa {6,4}₃ se puede ver como {6,4}_4,0. Seguir las aristas opuestas atravesará los 4 hexágonos en secuencia

Mapas regulares con característica de Euler cero[5]
g	Schläfli	Vértices	Aristas	Caras	Grupos	Orden	Notas
1	{4,4}_b,0 n=b²	n	2n	n	[4,4]_(b,0)	8n	Poliedros toroidales planos Igual que {4,4 \| b}
1	{4,4}_b,b n=2b²	n	2n	n	[4,4]_(b,b)	8n	Poliedros toroidales planos Igual que rectificado {4,4 \| b}
1	{4,4}_b,c n=b²+c²	n	2n	n	[4,4]+ _(b,c)	4n	Poliedros toroidales quirales planos
1	{3,6}_b,0 t=b²	t	3t	2t	[3,6]_(b,0)	12t	Poliedros toroidales planos
1	{3,6}_b,b t=2b²	t	3t	2t	[3,6]_(b,b)	12t	Poliedros toroidales planos
1	{3,6}_b,c t=b²+bc+c²	t	3t	2t	[3,6]+ _(b,c)	6t	Poliedros toroidales quirales planos
1	{6,3}_b,0 t=b²	2t	3t	t	[3,6]_(b,0)	12t	Poliedros toroidales planos
1	{6,3}_b,b t=2b²	2t	3t	t	[3,6]_(b,b)	12t	Poliedros toroidales planos
1	{6,3}_b,c t=b²+bc+c²	2t	3t	t	[3,6]+ _(b,c)	6t	Poliedros toroidales quirales planos

En poliedros toroidales generalmente regulares, {p,q}_b,c se puede definir si p o q son pares, aunque solo las configuraciones euclídeas anteriores pueden existir como poliedros toroidales en 4-dimensiones. En {2p,q}, los caminos (b,c) se pueden definir como pasos cara-arista-cara en línea recta, mientras que las formas duales {p,2q} verán las secuencias (b,c) como pasos vértice-arista-vértice en líneas rectas.

Véase también

Referencias

Coxeter (1980)
Séquin, Carlo. «Symmetrical immersions of low-genus non-orientable regular maps». Berkeley University.
Harold Scott MacDonald Coxeter 1980, 8.3 Mapas de tipo {4,4} en un toro.
Harold Scott MacDonald Coxeter 1980, 8.4 Mapas de tipo {3,6} o {6,3} en un toro.
Harold Scott MacDonald Coxeter y Moser, Generators and Relations for Discrete Groups, 1957, Capítulo 8, Mapas regulares, 8.3 Mapas de tipo {4,4} en un toro, 8.4 Mapas de tipo {3,6} o {6,3} en un toroide

Bibliografía

Coxeter, H. S. M.; Moser, W. O. J. (1980), Generators and Relations for Discrete Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete 14 (4th edición), Springer Verlag, ISBN 978-0-387-09212-6..
van Wijk, Jarke J. (2009), «Symmetric tiling of closed surfaces: visualization of regular maps», Proc. SIGGRAPH (ACM Transactions on Graphics) 28 (3): 12, doi:10.1145/1531326.1531355, archivado desde el original el 9 de junio de 2011..
Conder, Marston; Dobcsányi, Peter (2001), «Determination of all regular maps of small genus», Journal of Combinatorial Theory, Series B 81 (2): 224-242, doi:10.1006/jctb.2000.2008..
Nedela, Roman (2007), Maps, Hypermaps, and Related Topics, archivado desde el original el 4 de marzo de 2016, consultado el 8 de septiembre de 2022..
Vince, Andrew (2004), «Maps», Handbook of Graph Theory..
Brehm, Ulrich; Schulte, Egon (2004), «Polyhedral Maps», Handbook of Discrete and Computational Geometry..

Datos: Q7309606
Multimedia: Regular maps / Q7309606

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Coxeter (1980)

[csequin-2] Séquin, Carlo. «Symmetrical immersions of low-genus non-orientable regular maps». Berkeley University.

[3] Harold Scott MacDonald Coxeter 1980, 8.3 Mapas de tipo {4,4} en un toro.

[4] Harold Scott MacDonald Coxeter 1980, 8.4 Mapas de tipo {3,6} o {6,3} en un toro.

[5] Harold Scott MacDonald Coxeter y Moser, Generators and Relations for Discrete Groups, 1957, Capítulo 8, Mapas regulares, 8.3 Mapas de tipo {4,4} en un toro, 8.4 Mapas de tipo {3,6} o {6,3} en un toroide