Decaracto

En geometría de diez dimensiones, decaracto^{[cita requerida]} es el nombre de un miembro de la familia de los hipercubos, con 1024 vértices, 5120 líneas, 11520 cuadrados, 15360 cubos, 13440 hipercubos, así como 8064 penteractos, 3360 hexeractos, 960 hepteractos, 180 octoractos, y 20 eneractos.

Decaract (hipercubo-10)
Proyección ortogonal sobre un Polígono de Petrie
Tipo	Regular
Familia	hipercubos
Símbolo de Schläfli	{4,3⁸}
9-caras	20 {4,3⁷}
8-caras	180 {4,3⁶}
7-caras	960 {4,3⁵}
6-caras	3360 {4,3⁴}
5-caras	8064 {4,3³}
4-caras	13440 {4,3,3}
Células	15360 {4,3}
Caras	11520 Cuadrado
Aristas	5120
Vértices	1024
Figura de vértice	9-simplex
Polígono de Petrie	Isodecágono
Grupo de Coxeter	C₁₀, [3⁸,4]
Dual	10-ortoplex
Propiedades	Convexidad

Su nombre es el resultado de combinar (un acrónimo) el nombre de teseracto o hipercubo con el prefijo deca-[1] que se deriva del griego δέκα "diez" y significa diez (en este caso, diez dimensiones). También se le puede llamar icosaxennon o icosa-10-topo.

Es parte de una familia infinita de politopos $n$ dimensionales conocida como hipercubos. El politopo dual de un decaracto puede ser llamado un 10-ortoplex o decacruce, y es una parte de la familia infinita de los politopos de cruce.

Características

Puede ser nombrado por su símbolo de Schläfli {4,3⁸}, estando según esto compuesto de 3 eneractos alrededor de cada una de las 8-caras del decaracto.

Coordenadas cartesianas

Las coordenadas cartesianas para los vértices de un decaracto centrado en el origen y de longitud de arista 2 son:

(±1,±1,±1,±1,±1,±1,±1,±1,±1,±1)

mientras que el interior de la misma se compone de todos los puntos (x₀, x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉) con −1 < x_i < 1.

Otras representaciones

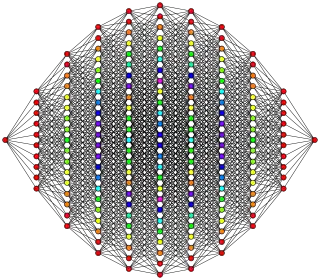Este grafo del decaracto es una proyección ortogonal. La orientación que presenta la imagen muestra columnas de vértices situados a distancia vértice-arista-vértice desde un vértice de la izquierda a un vértice de la derecha, y las aristas uniendo columnas de vértices adyacentes. El número de vértices en cada columna es equiparable al de las filas del triángulo de Pascal, siendo estas 1:10:45:120:210:252:210:120:45:10:1.	Polígono de Petrie, visto con una proyección ortogonal oblicua.

Proyecciones ortográficas del decaracto

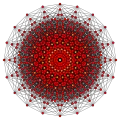
$B 10 {\displaystyle B_{10}} 20 vértices de borde$
$B_{10}$
20 vértices de borde
$B 9 {\displaystyle B_{9}} 18 vértices de borde$
$B_{9}$
18 vértices de borde
$B 8 {\displaystyle B_{8}} 16 vértices de borde$
$B_{8}$
16 vértices de borde
$B 7 {\displaystyle B_{7}} 14 vértices de borde$
$B_{7}$
14 vértices de borde
$B 6 {\displaystyle B_{6}} 12 vértices de borde$
$B_{6}$
12 vértices de borde
$B 5 {\displaystyle B_{5}} 10 vértices de borde$
$B_{5}$
10 vértices de borde
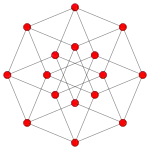
$B 4 {\displaystyle B_{4}} 8 vértices de borde$
$B_{4}$
8 vértices de borde
$B 3 {\displaystyle B_{3}} 6 vértices de borde$
$B_{3}$
6 vértices de borde
$B 2 {\displaystyle B_{2}} 4 vértices de borde$
$B_{2}$
4 vértices de borde

Politopos derivados

Aplicando una operación de alternación, eliminando vértices alternativos del decaracto, se crea otro politopo uniforme, el llamado 10-demicubo, (parte de la infinita familia de los demihipercubos).

Véase también

Portal:Matemática. Contenido relacionado con Matemática.
Portal:Geometría. Contenido relacionado con Geometría.

Referencias

Guide for the Use of the International System of Units (SI), 1995, NIST Special Publication 811

Bibliografía

H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  - (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  - (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre Decaracto.
Weisstein, Eric W. «Hypercube». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Multi-dimensional Glossary: hypercube Garrett Jones (en inglés)
"Sloane's A135289 : Hypercubes:10-cube", en The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. (en inglés)

Datos: Q2338993

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[SP811-1] Guide for the Use of the International System of Units (SI), 1995, NIST Special Publication 811